
DeepSeek 低调发布了 DeepSeek-Prover-V2,它结合 Lean 4,并用先进的思维链、深度学习方法,让计算机能像数学家一样,自动解决和验证各种数学难题,展示了大模型应用在数学领域的新的可能性。

形式化证明:让数学变得“可验证”
在深入 DeepSeek-Prover-V2 之前,必须先理解 “形式化证明” 这一概念。传统的数学证明往往以自然语言描述,虽然直观易懂,但容易出现歧义、遗漏细节,难以完全杜绝人为错误。而形式化证明的目标,是将每一步推理都用严格定义的符号语言表达出来,确保每一处逻辑都能被计算机自动检查。
形式化证明并不只是把普通证明 “翻译” 成编程语言那么简单。它要求证明者明确每一个前提、每一个推理步骤,不能省略任何细节。比如,证明 “若 a 和 b 都为偶数,则 a+b 也为偶数”,在形式化证明中,不仅要定义“偶数” 的数学含义,还要一步步推导出 a+b 满足相同的定义。这种细致入微的表达方式,为复杂的数学理论和工程系统提供了坚实的可靠性基础。
随着代数、分析、数论、计算机科学等领域理论体系的日益庞杂,手工完成形式化证明变得异常繁琐。因此,开发自动化的证明辅助工具,成为降低形式化门槛、提升科研效率的重要途径。Lean 4 就是当前最具影响力的形式化证明系统之一。
Lean 4:现代形式化证明的引擎
Lean 4 是由微软研究院主导开发的第四代 Lean 证明辅助系统。它不仅仅是一种编程语言,更是一个集证明环境、交互式验证器、元编程平台于一体的强大工具。Lean 4 的设计哲学是让用户既能像写代码一样高效地表达严谨的数学证明,又能通过自动化手段大幅提升生产力。
Lean 4 其实可以理解为一种“聪明的数学编程语言”和证明工具。它的底层原理很严谨,但用起来却很灵活简单。Lean 4 结合了数学逻辑推理和编程的好处,让我们既能用简洁的方式写出各种数学概念和公式,也能很方便地实现复杂的自动化证明。
Lean 4 有个非常实用的功能叫“战术式证明”,你可以像下棋一样,一步步用指令推动证明的进展,每走一步,系统都会帮你检查和提示。Lean 4 还自带了庞大的数学知识库(比如 Mathlib),里面包含了各类高等数学的内容,为自动化证明提供了丰富的“现成工具”。
Lean 4 的另一个优点是高度灵活和易扩展。你可以像写程序那样,自己定义新的数学对象、定理甚至证明方法。如果你有特别的需求,还能通过 Lean 的“元编程”功能,打造属于自己的自动化工具。这种设计大大降低了学形式化数学的难度,让更多人都能轻松上手。
在使用体验上,Lean 4 能和常用的代码编辑器(比如 VS Code)无缝结合。你每输入一步,Lean 4 都会马上反馈当前的证明进度,比如还剩哪些目标、有哪些已知条件可以用等。这种“边写边看、边学边试”的方式,让学习和使用 Lean 4 变得直观又高效。
最后,Lean 4 最被信任的地方在于它有一个严格的“内核”检查机制。无论你写多复杂的证明,Lean 4 都会一条一条帮你核查,确保每一步都没有逻辑漏洞。正因为这种严谨性,Lean 4 写出的数学内容非常可靠,已经被很多国际大型项目选为数学知识的标准平台。
在 DeepSeek-Prover-V2 项目中,Lean 4 是整个形式化证明生成与验证的底座。模型最终输出的证明代码,都严格遵循 Lean 4 语法规范,可以直接被 Lean 4 系统检查、运行与复用。这不仅确保了证明的正确性,也为后续数学知识的积累与共享打下坚实基础。
子目标分解:复杂问题的巧妙拆解
现实世界中的数学难题,往往并非一步到位即可解决。高效的数学家通常会将一个复杂目标分解为若干个更容易处理的子目标。这类似于解决难题时 “分而治之” 的策略:每个子问题都有独立的解法,最后再将这些 “小证明”拼接起来解决整体问题。
在 DeepSeek-Prover-V2 的自动证明流程中,子目标分解是核心环节。模型首先读取到一个需要证明的 Lean 4 定理,会先尝试自动分析并拆解出一系列子目标。每个子目标要么是原问题的一个具体化步骤,要么是一个辅助引理的证明。经过递归分解,原本晦涩难解的大题被拆成多个环环相扣的 “小台阶”,模型只需逐步往上走,最终就能完成整体证明。
这种策略极大降低了大模型的推理难度,同时也让数据生成更高效:每个子目标都可以独立并行训练和验证,便于大规模自动化数据积累。而且,子目标分解天然契合数学“层层递进”的思维方式,更贴近人类解题习惯。
思维链(chain-of-thought):让推理过程变得透明
思维链指的是模型在生成答案前,先输出自己的推理过程和中间步骤。这一机制不仅让模型的决策更具可解释性,也有助于提升其解决复杂问题的能力,而这项功能在数学证明过程中尤为有用。
在 DeepSeek-Prover-V2 的训练和推理中,chain-of-thought 扮演了桥梁作用。每当模型接到一个问题时,不是直接给出最终证明代码,而是先生成一份详细的推理计划。这份计划通常包括如下内容:
- 明确要证明的目标
- 需要用到的定理或引理
- 每一步的推理思路和证明结构
- 关键的数学工具或方法
比如,在证明一个代数等式时,模型会先写出:“第一步,将等式两边同时乘以 x;第二步,合并同类项;第三步,利用已知引理……” 这样的思维链,不仅让模型的思路更加清晰,也便于后续的自动化验证和错误追踪。
更重要的是,思维链能作为训练数据,帮助模型学会 “思考” 的习惯。研究表明,经过思维链训练的模型,往往比直接输出结果的模型更擅长解决需要多步推理的难题。
强化学习:让模型自己“摸索”高分策略
传统的机器学习多依赖于监督学习,即 “模仿” 人类专家的答案。而强化学习(Reinforcement Learning, RL)则让模型在交互环境中,通过“试错”不断提升自身策略。模型每做出一步行动(如生成一个证明步骤),环境会给出奖励或惩罚,最终促使模型学会最优行为序列。
在 DeepSeek-Prover-V2 中,强化学习被用于模型训练的后期阶段。团队首先利用自动生成的思维链 + 形式化证明数据对模型进行冷启动训练(冷启动训练就是让模型在“什么都没有”的起点,通过自动化手段先积累起最初的知识,为后续更深入的学习做好铺垫。它是大模型发展的关键第一步。),然后进入强化学习阶段,让模型根据 “证明是否正确” 这一二元反馈继续自我优化。每当模型生成的证明能被 Lean 4 成功验证,就获得正向奖励。如果失败,则没有奖励。通过大量的自动化试错,模型能逐步掌握高效、正确的证明策略。
这种训练方式极大提升了模型的泛化能力,使其不再局限于模仿已有样例,而是真正 “学会” 如何拆解新问题、选择恰当方法。这也是 DeepSeek-Prover-V2 能在 MiniF2F、PutnamBench 等基准测试中取得优异成绩的关键。
DeepSeek-Prover-V2 的数据与基准集:为行业树立新标杆
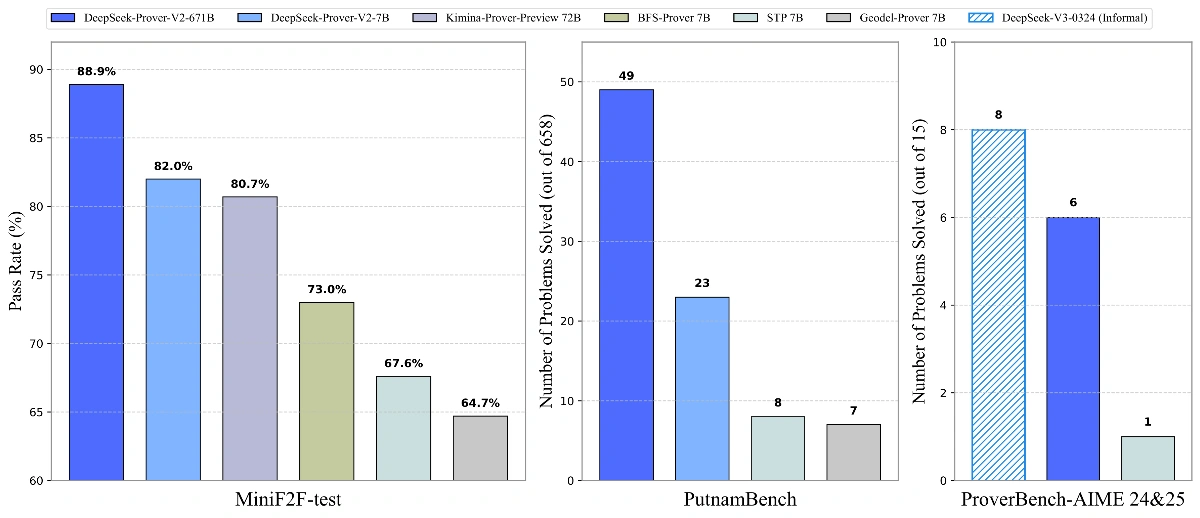
DeepSeek-Prover-V2 的强大不仅体现在模型结构和训练流程上,还得益于其高质量、覆盖面广的数据集。项目团队发布了名为 ProverBench 的基准数据集,囊括了 325 道多样化的数学题目,包括:
- 近期 AIME(美国高中数学邀请赛)上的数论与代数题
- 经典教科书中的基础例题
- 各类解析、线性代数、概率、抽象代数等领域的代表性问题
这一基准集的建设,使 DeepSeek-Prover-V2 的评测更加全面,既能考察模型在竞赛级难题上的表现,也能反映其对基础数学知识的掌握。并且,所有模型、数据、证明样例均已开源,为学界和业界的二次开发和对比研究提供了便利。
DeepSeek-Prover-V2 的整体流程与技术创新
综合来看,DeepSeek-Prover-V2 的工作流程大致如下:
- 数据生成:通过 DeepSeek-V3 及小模型,自动递归分解原始定理为多个子目标,生成推理链与对应的 Lean 4 形式化证明
- 冷启动训练:利用自动生成的数据对大模型进行初步训练,掌握基本的证明思路、分解策略与正式表达
- 强化学习微调:进入强化学习阶段,让模型在 “成功/失败” 的自动化反馈中进一步优化其证明能力
- 自动验证与评测:利用 Lean 4 系统自动检查模型输出,确保每一步证明都严格正确
- 开放下载与社区共建:模型、数据、基准全部开源,便于学界、工业界共同推动形式化证明自动化
DeepSeek-Prover-V2 的技术创新,体现在以下几个方面:
- 有效融合思维链与形式化代码的生成,兼顾可解释性与机器验证性
- 递归子目标分解大幅提升了复杂问题的求解效率
- 强化学习让模型具备了自我进化、自主探索的能力
- 全程适配 Lean 4,确保输出证明的严谨与复用性
- 构建了高质量、多领域的基准数据集。
实际应用与未来展望
DeepSeek-Prover-V2 的落地场景非常广泛。对于数学研究者而言,它能自动生成复杂定理的详细推理和形式化证明,辅助理论创新和知识验证。对于教育领域,自动生成的思维链计划和 Lean 4 代码,可以作为教学范例,帮助学生理清解题思路、掌握形式化技术。对于工程师和系统开发者,DeepSeek-Prover-V2 还能用于形式化验证算法、协议、程序正确性,为高可靠性软件系统保驾护航。
更值得期待的是,随着模型与数据的持续扩展,DeepSeek-Prover-V2 有望服务于更广阔的“数学自动化”生态。比如,协助人类专家探索尚未解决的难题,参与大型知识库的自动化建设,甚至为 AI 系统的安全性和可靠性提供理论支持。
DeepSeek-Prover-V2 以其先进的递归分解策略、chain-of-thought 推理链、强化学习优化以及对 Lean 4 的深度适配,推动了自动定理证明与形式化数学的智能化进程。它不仅实现了从 “思路” 到 “代码” 的完整闭环,更通过开源推动了整个领域的技术创新与知识共享。未来,随着更多数学知识被形式化、更多模型能力被解锁,自动化证明工具有望成为数学、科学、工程等领域不可或缺的基础设施,为人类认知与创新插上智能的翅膀。
DeepSeek-Prover-V2 项目地址:https://github.com/deepseek-ai/DeepSeek-Prover-V2
